Energy
Exploration Pages
Photosynthesis Intro
Page
Energy Flows Through Life
Other FT Exploring Pages
Dr
Galapagos
What
is an Engineer, Really?
Site Map
Link
Pages
Lesson
Plans
Contact
Me
|
|
| |
Wind
Turbines and the Energy in Wind
 I
like wind turbines. They're interesting to me, even the little ones. But the big ones,
well, with apologies to Walt Whitman, "I can stand and look at them long
and long". Wind energy and wind turbines were among my first interests as
a beginning engineer and I hoped to work in that field. In those days, though,
jobs in alternative energy were scarce (to protect
my privacy and illusions of youth, we won't say when those days were).
A wind turbine is a device for converting the kinetic
energy in wind into the mechanical energy of a rotating shaft. Usually that
rotating mechanical energy is converted immediately by a generator into electrical
energy. In the large turbines, such as those shown in the picture above, there
is generally a generator on top of the tower. The generator is usually connected
to the turbine shaft through gears which turn the generator at a different speed
than the turbine shaft. Fancy power electronic controls convert the electricity
into the correct frequency and voltage to feed into the power grid (probably 60
Hertz or 50 Hertz depending on which country you live in).
The first law of thermodynamics tells
us the energy out of the wind turbine over a certain amount of time (power) has to equal the energy that went into the turbine during the same amount of time (also power). The "energy in"
is the kinetic energy from the wind's velocity and air density that flows into the area swept by the turbine blades. It is not possible
to convert all of the wind's kinetic energy into mechanical energy. Some energy
must remain in the air leaving the turbine. The "energy out" is the energy converted by
the turbine blades into mechanical energy (which is then usually turned into electricity), plus whatever energy is left in the
air after it passes through the turbine rotors.
 How
much energy is in the wind? And how much of that energy can a wind turbine "catch"?
Oops, I mean how much of the wind's energy can a wind turbine convert
into useful electrical energy? As with all real devices, wind turbines have their
limitations. We can't get it all.
The not-exactly-Picasso colored pencil drawing at the right is my attempt to show the "tube"
of wind energy that goes into a wind turbine. The "D" represents the
diameter of the turbine blades. The blue oval is to show that the circular area
of wind swept by the blades is the area available for producing power. Kinetic
energy is a function of mass and velocity. So to know the energy in the
wind we have to know the wind's velocity as well as the density of the air. The
density is the mass per unit volume (kilograms per cubic meter [kg/m^3], or pounds
mass per cubic foot [lbm/ft^3] are a couple of typical examples of units of density).
Of course, what we are really interested in as engineers and producers or users
of electricity is the power we can get out of the wind. Power is how fast we are
producing or converting a quantity energy. Power has units of energy divided by time.
A Watt is a unit of power. It represents one joule of energy transformed every
second. A 60 Watt light bulb converts 60 joules of energy every second into light
and heat (mostly heat - don't touch the bulb).
The formula below shows the variables that determine the power in the wind going into the wind turbine (not the power
obtainable, because we can't get it all):
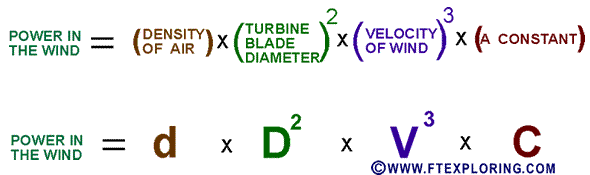
Notice that the power in the wind going into a specific wind turbine, depends on 3 variables, the density of the air, the diameter
of the turbine blades squared (D times D), and the velocity of the wind to the
third power (V times V times V). There is also a constant (not a variable) in there which I'll
discuss a little in the very next paragraph.
 What
about that constant, C? It's placed off by itself because we wanted to just show the variables that determine wind power. It is actually a combination of two or more constants, depending on the specific variables and system of units you want to use.
Part of the constant comes from using D to calculate the Area swept by the blades of diameter, D. The area is calculated by multiplying
the number Pi (approximately 3.14159) times the diameter squared divided by 4.
So part of the constant C, is just the constant number Pi divided by 4 pulled
out to show us that the variable
in the area formula is D. Another part of the constant C, can be whatever unit
conversion numbers are needed to make sure the numbers come out right. This will depend on the system of units you use, and whether you want to throw in other units like miles per hour rather than meters per second, or slugs instead of kilograms. And lastly, a reader recently reminded me I should point out there is always a 0.5 in there that comes from the expression for kinetic energy that is part of the derivation of the formula.
For now,
we won't go further into that. The point for this page, is that the variables that determine
the wind power blowing into a wind turbine are air density, blade diameter
(resulting in a certain swept area), and wind velocity. Some day a page will come with examples of how to use the formula with different systems of units.
| |
You
have probably noted that power (not energy) is dependant on the velocity times
itself 3 times (V x V x V). Whoa! In other words, if the wind speed doubles, the
power available from the wind increases by a factor of eight. The diameter is
significant too. Doubling that increases the power by 4 times. Faster is better,
and bigger is better (if you can afford it and can build it strong enough).
Of course, the wind doesn't blow all the time in most places and when it blows
too hard the turbine blades can break or spin so fast they break off (not good
when each blade can weigh several tons). In that case, the blades are usually
"feathered" to reduce stresses on them and to slow them down. This means
we can't take advantage of really high wind speeds.
Turbine Efficiency
If the turbine could convert all the wind's power to mechanical power we would
say it was 100% efficient. But as you probably know, the real world is never so
generous. To even achieve 50% is unlikely, and would be a very efficient machine.
A 50% efficient turbine would convert half of the power in the wind to mechanical
power.
This link has more on
Wind Turbine Efficiency
.
|
|
|
|
Is
It a Mill or a Turbine?
Sometimes they are called windmills but wind turbine is better. A mill is place
where they grind grain, usually for making flour for baking bread. In times past,
water mills and windmills were places where the power in water or wind were used
to turn big stones for grinding grain.
Small windmills are still commonly used to pump water out of the ground, often
to fill small tanks of water for livestock to drink. A better name for them might
be wind-pumps or wind-wells.
A turbine is a device for converting the energy in a moving fluid into
mechanical rotating energy. There are big turbines at the bottom of dams that
convert the energy from pressure and velocity in water into rotating mechanical
energy to drive huge generators. There are turbines in jet engines and turbochargers
that convert the velocity, pressure, and temperature, in engine exhaust gasses
into mechancal energy. After going through the turbine the exhaust gas is cooler
and has a lower pressure. There are steam turbines that convert the pressure and
velocity and high temperature of super-heated steam into mechanical rotating energy
to drive electric generators.
Wind turbines only take velocity or kinetic energy out of the wind. It's only
the kinetic energy of the moving air molecules that we can convert to mechanical
energy. |
|
 |
|
|
|
|
|
|
The
Bad News Betz Law
First there is the little piece of bad news called the Betz' law. Back in 1919
a smart German physicist named Albert Betz figured out that the most you can possibly
get out of wind turbine is around 59% of the power in the wind. This is an unassailable
bit of physics. Stop whining about it. I'm not going to prove it here but it is
not hard to at least understand why we can never convert 100% of the wind's power.
 Imagine
a wind energy extraction machine of 100% efficiency that could take all of the
kinetic energy out of the wind. That would mean the velocity on the "out"
or "leaving" or "exit" side of the turbine blades would be
zero, zilch, zed, nothing. No kinetic energy left in the wind. No velocity left
in the wind. No wind. Dead calm. The doldrums.
Get Out of the Way
If the velocity leaving the blades is zero then the air wouldn't be leaving at
all. There would be no air movement, meaning the air after the blades isn't getting
out of the way of the air coming in, which would mean the fresh air couldn't come
in, which would mean there is no air flowing through the turbine blades, which
would mean no power. In order to at least keep the wind moving through the turbine
there has to be some velocity or energy in the air after going through the blades
so that the air can get out of the way of the air coming through next. Sort of
a "Catch-22". Just to keep the machine running at all the efficiency
has to be less than 100%.
Mr. Betz pointed this out and then proceeded to prove, with solid physics and
math, that the best that could be achieved by a wind turbine is around 59%. In
other words, a perfect best-possible wind turbine would be able to convert almost
59% of the power in the wind into mechanical rotating power. But we can't achieve
perfection. There are other things that limit efficiency, and efficiency may not
even be the most important thing. The most important thing is generally to get
the most electric power for the least money. This may require design trade-offs
that limit efficiency in order to get the best overall system for the money. For
example, it might not be possible to make the most efficient blade shape strong
enough to hold together during a strong wind. As you can see from the formula
above, being able to get power from a stronger wind is probably worth more than
efficiency. On a very windy site, stronger less efficient blades might end up
getting us more power. This is typical. Engineers have to deal with conflicting
design trade-offs all the time.
Efficiency Varies with Wind Speed
A given wind turbine has a "design point" that generally defines its
peak efficiency at the wind speed for which the system is designed. At wind speeds
above and below the design speed the efficiency is the same or less - maybe much
less. If a turbine's best efficiency is 40% at a wind velocity of 9 meters per
second (about 20 mph), it will be 40% only at that wind speed. At all other wind
speeds it will be something worse. That wind turbine will generally operate at
lower than its best efficiency, because wind speeds are never constant or average.
The electric power actually produced will be still lower because the generator
efficiencies are also less than 100% (generally in the mid- or low-90's at best),
and there are further losses in the conversion electronics and lines. But this
is true of all power technologies. When all these losses are figured in, you might,
if you are lucky, be getting 35% or so of the wind's energy actually delivered
as useful electrical energy to the end user in the very best conditions. The average
might only be in the twenties.
In the formula above, then, we have to add one more number that I don't show.
That number is an efficiency number that would have to supplied by the manufacturer
of the wind turbine, or experimentally determined by you if you make it yourself.
It will not be one number, but a variable that is a function of wind speed.
|
|
| |
If this page has been helpful, please share:
|
|
| |
First
Law of Thermodynamics The Energy
Intro Page Energy Conversions
>>
|
|
| |
The
Second Law of Thermodynamics |
|
|
|
|
|
|
|
