 |
|
Variable Variations
Question:
Dear Dr. Galapagos,
Whatis the difference between independent and dependent variables?
R G Reynolds |
|
|
 |
|
|
 |
|
|
| Answer
to Question: |
Dear
Mr. Reynolds,
Your question intrigued me. No secrets of the universe for you (come to think
of it, no one has sent in a secret of the universe question). Just a simple math
problem. If this is a homework question, you may be dissapointed. Dr. Galapagos
is not celebrated for his celerity, only for his slow cerebrum (sorry I couldn't
stop myself ). You will probably be doing
advanced differential equations by the time you get my answer.
I felt mysteriously compelled to answer this question from among the thousands
(not!) we have received. But I'm not just going to talk about variables, I'm going
to digress and ramble. I'll throw in a couple of famous equations with slight
digressions on Pi and the Mysterious
Everything (just to confuse you). |
|
 |
| |
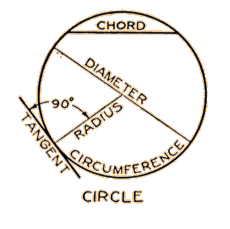
The
above picture has nothing to do with Mr. Reynold's question, but is helpful when
considering our first formula example. The diameter is the distance across the
middle of the circle. The circumference is the distance around the outside of
the circle. |
|
|
|
We are talking about the
dreaded M word (Math) here, right? And even worse, the dreaded A word (Algebra)?
For most of us, examples are the best way to learn, so here come two examples.
I'm afraid we will have to assume some knowledge of algebra
and equations for this, in order to be able to answer in a reasonable amount of
words.
|
|
|
Circles
Take a formula, any formula (or equation). The following famous formula is true
for any and all true circles:
Pi = C / D
C is the Circumference (distance around the outside) of the circle.
D is the Diameter (distance across the middle) of the circle.
(I have to
spell out Pi, rather than use the Greek letter, because some browsers - we won't
say which, but they know who they are - don't show the symbol properly.)
|
|
 |
| |
The
dancing tiger whirled in endless circles, never once stopping to consider the
significance of Pi, or the difference between dependant and independant variables. |
So if you want to say the above famous formula in not-so-plain English, you could
say that "Pi equals the circumference of any circle divided by the diameter
of that same circle"; or you could say "Pi equals the ratio (a fancy
way of saying divided by) of the circumference to the diameter". What's that
got to do with variables? Nothing. |
|
|
|
KEEP GOING, IT'S NOT REALLY THAT BAD.
You can't read this stuff like an Archie comic (nothing against Archie comics,
I love 'em). You have to go slow and think about it. You may even have to read
it all twice. This is math, you have to do problems and think about it. |
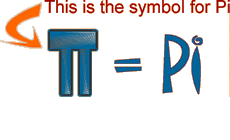 For
all circles, no matter what the size, the number Pi is always the same. Pi is
always 3.141592654....and on and on and on and on for millions and millions of
places. Let's keep it simple, though, and say Pi equals about 3.14 - close enough
for explaining variable variations.
Pi is a constant. It never changes (except for how many decimal places you choose
to write). It is always the same. IT IS A CONSTANT!
|
|
|
| Where
Are the Variables? |
The other two guys, the C and the D, are the variables. They can vary. They can
change. They are variables! Formulas always have variables. At least all
the formulas I know.
Now let's shuffle the variables around. If you aren't too familiar with algebra,
take my word for it that I can do the following and it is still the same true
formula:
C = Pi x D
or C = Pi times D
or C = Pi D
Or in English, the Circumference of a circle equals Pi times the Diameter of the
circle.
Remember that Pi is a constant. It always equals 3.14.
|
|
 |
| |
The
guys who put the big circles all over the earth often considered the usefullness
of Pi and probably also knew the difference between Dependant and Independant
variables. |
|
|
|
But what are the other two guys - the C and the D? You remembered!
They are variables. They can vary.
Which brings us to Mr. Reynold's question. One of the above variables is a DEPENDENT
variable and one is the INDEPENDENT variable. (Kind of like "What's
My Line", isn't it?). Can you guess which is which? Not quite enough clues
yet?
|
|
|
 |
|
When
a formula is written this way,
C = Pi x D, it is said that C is a function of D, which is a "math talk"
way of saying that the value of C depends on D, or is DEPENDANT on D. Since
we are solving for C, we can't know what C is until we first know what D is.
If we say D is 1 (since it's independent we can say it's anything we want), then
C has to be equal to 3.14 times 1, or 3.14.
If we say that D is 2, then C must be 3.14 times 2, or 6.28.
If we say that D is 3, then C must be 3.14 times 3, or 9.42.
See, we can put any number we want into D, because it is independent. It is the
independant variable. |
Even
though she could make nearly perfect circles in her web, the spider knew nothing
of Pi or the difference between dependent and independent variables.
|
|
We gave it
a declaration of independance by putting it on the right side and putting C off
all by itself on the left.
We put C in chains and said, "Mr. C you must be dependant on D. You're value
is a function of Mr. D. You are dependant on him. You have no value without D.
Why? Because we say so. Because that is the way we wrote the formula." |
|
|
|
But what if Mr. C says, "I don't like always being dependant on D. I must
be free. Let me be independant at least some of the time."
Okay, no problem. But somebody has to be dependent.
We'll just rewrite the formula, like so -
D = C / Pi, or the Diameter is equal to the Circumference divided by the Constant
known as Pi. Now we are solving for D.
Or, listen to this. We could say, "the value of the Diameter is DEPENDENT
on the value of C divided by Pi. If we talked like that it might be easier to
get the hang of this.
This is still the same formula. But now D depends on C (Pi is still an unchanging
constant). D is now the dependent variable and C gets to be the independent variable.
All that means is that we can put any number we want in C, but D can only be determined
after we know what C is. D is dependent on C, and C is free at last.
Another
Formula, Another Example
 Confused?
How about another example with another famous equation. The one that everybody
quotes (but not so many understand).
Yup, it's Einstein's e = mc². It says that matter and energy are equivalent,
a statement of the Mysterious Everything,
if you will. This is a cool formula, worth contemplating, but we are discussing
variables, aren't we, not the wonders of the universe. So for our purposes this
is just another algebra equation with some variables to define.
|
|
|
This
equation can also be written in different ways, depending on whether we are solving
for e (energy), or m (mass). In this case, c (the speed of light) is a constant.
You don't always have to have a constant in a formula, but it is pretty common.
So e and m are the variables. Which one is the dependent variable and which one
is the independent variable? We are solving for e in this case so e is dependent
on m. m can be any value we need it to be, while e has to wait on m. It's getting
easy now isn't it? The independent variable is m. The dependent variable is e.
|
|
 |
| |
Albert
knew he would never be truly happy until a galapagos tortoise used his formula
to explain the difference between dependent and independent variables. |
|
|
|
|
|
Of course, though it is not usually done for us laymen, we can write it so that
we are solving for m:
m = e / c² or (mass = energy divided by the speed
of light squared)
Now m is dependent on e. The dependent variable is therefore m and the independant
variable is e.
Getting pretty tired of this? Let's summarize and wrap it up with one more example.
In an algebra equation
the variable you are solving for is the dependent variable. The other variable
or variables (there can be lots of variables) are independent. As far as most
algebra equations are concerned, any number can be put into an independent variable
(not always true, of course, in the real world) but the dependent variable can
only be known after a value is given for the independent variable(s).
One Last
Example
Look at this example of a
more typical looking algebra equation:
y = 2 + 5x - 6z + 3x² - 12w³
Wow. Lots of numbers and letters and powers but it is still just an algebra equation.
In MATH TALK we would say that y is a function of the variables x, z, and w. The
value of y is dependent on x, z, and w. So y is the dependent variable, and x,
w, and z are all independent variables.
Ta Da! The End. If you read the whole thing you should reward yourself with a
nice cold bowl of ice cream to help you wake up.
Send your comments.
Home Page
Next Dr. Galapagos Question: Who Uses Carbon Dioxide?
Site Map
Top of the Page
|
|
|
|
|
