Wind Turbine Efficiency

Wind Turbine Efficiency - What it's for and not for

"Typical power transmission path in a large wind turbine."

Wind turbine efficiency is used to compare the performance of wind turbines to other wind turbines. That's all.

What does the efficiency of a wind turbine have to do with the efficiency of a diesel engine or coal-fired steam power plant?

Nothing! Absolutely nothing!

Though you may see it done on the internet and elsewhere, you can't compare, on the basis of efficiency, wind turbines to diesel engines or solar cells or any other type of non-wind power producing systems. There are, of course, meaningful ways to compare them, but efficiency is not one.

This page explains how the efficiencies of wind turbines, and what I will call "heat-converting" engines, are calculated. Along the way it will become clear why they are not comparable.

What is Efficiency?

The word efficiency is used to describe precise measurable physical concepts as well as non-technical, or even poetic, concepts. The non-technical concepts for efficiency are subjective and impossible to define with formulas. You don't, for example, hear ballet reviewers say, “the dancer had a beautiful efficiency of movement divided by the coefficient of spandex times 23.69 times Pi”.

In science and engineering, however, a particular type of efficiency must be defined with a clearly defined mathematical formula. This specific and clearly defined formula is generally used to compare the performance of a device or system to a specified ideal or standard of perfection. There are many efficiency formulas that define many different types of efficiency.

This can cause confusion for laypersons. It's the same word and a similar sort of idea, but with different formulas that define and measure different parameters. It is a useful tool for comparing machines, systems, or processes. The comparison generally holds only for the limited case for which it was intended.

To paraphrase my seventh grade shop teacher: "Use the right efficiency (tool) for the right system (job)".

The Formula for Wind Turbine Efficiency

As stated above, efficiency can be a useful way to compare the performance of a device or system to a mathematically defined ideal or standard of perfection.

For the wind turbine, one standard of perfection would be the ability to convert all of the power available in the wind passing through its blades, at a specific velocity, into useful mechanical power. This is the ideal, the best performance that can be imagined. An efficiency of 100% would mean that every last bit of available power in the wind passing through the turbine blades would be converted into mechanical shaft power. But remember, as is often the case with an ideal that can only be imagined, it is impossible to achieve. A wind turbine with an efficiency of 100% is impossible.

The answer to the formula will be a fraction. On the top (numerator) will go the expression for actual measured shaft power out of the turbine. On the bottom (denominator) will go the available wind power into the blades. The answer will always be some fraction or decimal less than 1 (considerably less than 1), and greater than or equal to zero. Zero would be a pretty lousy turbine - or broken. If you prefer percentages, then the number must be less than 100%. Remember that we're comparing to an ideal standard of perfection, and perfection is only attainable in our imaginations.

In terms of power, the formula, for just the turbine blade conversion efficiency (aerodynamic efficiency), will look like the expression below:

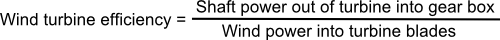
For a wind turbine the available power is almost entirely from the kinetic energy of all those trillions upon trillions of air molecules moving along together in that mass movement of air molecules we call wind. Thus the expression for the bottom part of the fraction above would be the wind power formula also described in another page, and shown below:

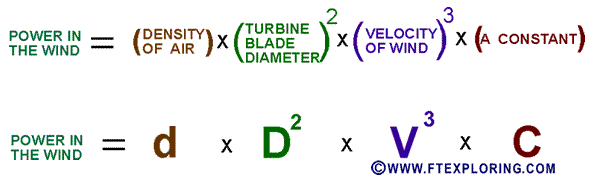
Don't worry about the constant for now. It is determined by several things, including the choice of units. I will explain that on another page. The point of the above formula is that the power available in the wind is a function of three variables: the air density, the blade diameter squared (assuming a conventional bladed turbine), and the cube of the wind speed.

This so-called "available power" in the wind is what, for this type of efficiency, we choose as our standard of perfection. To this imposible-to-achieve standard we will compare the measured performance of an actual real wind turbine. As stated previously, there is no way any wind turbine can convert all of the kinetic energy "blowin' in the wind". Just as it is impossible for any hydro-carbon fueled engine to convert all of the chemical energy stored in the fuel into useful energy (2nd Law of Thermo).

Would It be Better to Use Electrical Power Out?

For simplicity sake, I show the measured power out as the shaft power directly from the turbine that is delivered into the turbine drivetrain. You could, and should, make the argument that what really matters is the electrical power actually generated by the turbine and delivered to the electric power grid. The formula above really only evaluates the efficiency of the turbine blade design.

This is sometimes called the aerodynamic efficiency to indicate it only describes the performance of the turbine blades. I have also seen aerodynamic efficiency (in at least one source) referred to as Coefficient of Performance and designated with the same Cp used for the Power Coefficient described below. (Which all goes to show that we always need to make sure we understand the exact formula and variables we are looking at or using. Sometimes different formulas have the same name and vice-versa).

The actual electrical power out is determined not only by the blade performance, but also by the efficiency of the drivetrain (mechanical efficiency), and the electrical system which comprises mainly the generator and power electronics (electrical efficiency). The often used industry term Power Coefficient, and designated Cp, takes into account all of these efficiencies.

If you are paying for an actual wind turbine, other factors such as the specific turbine's power curve (electrical power out vs wind speed), the site's wind profile, and the predicted Capacity Factor (CF) of the site and system combined, will be of more importance to you than the efficiency. Those parameters, and others, will determine the amount of electricity your investment will actually produce over time.

But that is not what this page is about. This page is a simple explanation of the wind turbine efficiency concept and how it does not compare to other power source efficiencies. The summary at the end of this page explains more.

Thermal Efficiency

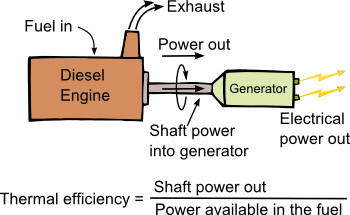
An engine that converts heat energy into useful mechanical energy, is often called a heat engine. A diesel engine, while not a true heat engine in the strict thermodynamic definition of the term, does convert heat generated by the combustion (burning) of diesel fuel into mechanical energy.

Thermal efficiency is a common and useful parameter for comparing the performance of heat engines. When well-meaning (let's give them the benefit of doubt), but misinformed, people compare wind turbine efficiency to other power sources, this is usually the type of efficiency they are quoting.

Thermal efficiency is generally calculated by dividing the actual measured mechanical power delivered to the shaft out of the engine by the power available in the fuel. If all of the thermal power (thermal energy converted per unit of time) released during combustion of the fuel in the engine were converted into useful shaft power, the engine would be 100% efficient. This would be perfection and, of course, is absolutely impossible (2nd Law of Thermodynamics).

Diesel engines, as heat engines go, are very efficient, but most of the thermal energy in a typical diesel engine still does not get converted into useful shaft power. Internal friction heats up the engine lube oil, the high temperatures of combustion heat up the engine parts which must be cooled by letting the heat flow into the cooling water, lube oil, or surrounding air, and the rest goes out with the hot exhaust. A very efficient large locomotive diesel engine only converts 40 to 45% of the available fuel energy into useful power at the shaft.

Steady-state energy flow rates in a typical modern diesel engine. In the example above 41 percent of the available energy (chemical energy in the diesel fuel) that is burned in the engine cylinders each hour is converted to useful power (power is the rate of energy conversion).

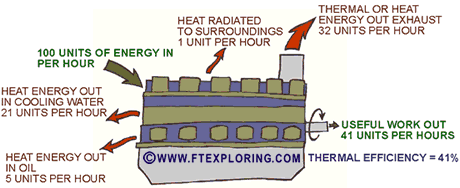
That's a very good energy conversion efficiency for this type of engine. Diesel engines are common because they are generally one of the most efficient types of heat engines.

But many other power sources can be considered heat engines, and can be compared on the basis of thermal efficiency.

Fair game for thermal efficiency comparisons are steam power plants, old time steam locomotives, car engines fueled by gasoline or other combustible fuels, large gas turbines, and more. All of these power producing systems create heat by burning some type of fuel, and thus can be compared on the basis of thermal efficiency.

However, once again, do not fall into the trap of over-simplifying and misleading yourself and others (lest people mistake you for a politician). There are other important parameters that may be relevent, such as the cost of the fuel, the type and amount of emissions from the fuel, the sustainability of the fuel, etc.

Summary and Final Thoughts on Wind Turbine vs. Heat Engine Efficiency

So why would anyone compare wind turbine efficiency to a heat engine efficiency? The heat engine burns fuel to create thermal energy which is then converted to mechanical work, while the wind turbine converts moving air molecules into rotating mechanical work. It should be clear that such a comparison is nonsensical.

And why have I bothered to do a whole page on this subject?

First answer: I generally see this comparison being made as part of an argument for, or against, wind energy. I suppose, assuming good intentions, it is just ignorance that would lead someone to make such a comparison. Whether through ignorance or deviance, though, it is pointless and misleading.

Second: I made this page because during the more than 10 years since I first put up my page on the wind power formula, I have observed people in web pages, internet discussions, blogs, etc., refer to my page in arguments both for and against wind energy.

That in itself is a little strange, since the page was not intended as an argument either way. But what really irks me, is that frequently people quote, out of context, the wind turbine efficiencies I mention on that page, as part of a comparison to some type, or several types, of heat engine thermal efficiencies.

This is my little attempt to set the record straight. If you come across a source or person making this misleading comparison. Set them straight. Send them to this page.

Efficiency Varies & There are Better Wind Turbine Comparison Tools

As a Post Script, since to oversimplify is to mislead, it's worth a quick minute to also remind ourselves that efficiency for both wind turbines and heat engines is a moving target. Efficiency for wind turbines varies with a number of parameters, such as: wind speed and direction, turbine rotational speed, and turbine blade pitch. The large vertical axis turbines typically adjust blade pitch as wind speed varies to optimize efficiency; and as wind velocity increases above the maximum power point, the pitch is varied to maintain constant power and a safe tip speed. Obviously, if the turbine power remains constant while the available wind power increases, the efficiency has to go down.

The same is true of diesel and other thermal types of engines. Engine efficiency will vary with engine speed, load, and transients. Changes to air inlet temperature and pressure can also have a significant effect. Thus a car on a hot day high in the mountains, will not perform the same as it does at the same temperature at sea level. And, just as with wind turbines, we have to limit the actual power an engine can deliver in order to keep it from falling apart sooner than the customer would like.

Responsible manufacturers of wind turbines and diesel engines, carefully measure and/or calculate delivered power at a wide range of operating conditions, and provide it to customers - well some of it.

If you are making such comparisons based on manufacturer or supplier data and quotes, make sure you completely understand what you are looking at, or find someone who does. The comparisons may not always be apples to apples.

Finally, as many readers will know, there are other wind power comparison tools, such as capacity factor and wind power curves that are also important. The power curve, which generally shows the electrical power output versus wind speed will, of course, be a function of the entire wind-power-system's steady-state efficiency at each wind speed. The capacity factor is not related to efficiency. It is determined by the wind characteristics of a particular site, as well as the availability of the wind turbine or turbines being evaluated.