Energy
Exploration Pages
Photosynthesis Intro
Page
Energy Flows Through Life
Other FT Exploring Sections:
Solar Energy!
The Definition of Life!
Biology & Cell Metabolism!
Dr Galapagos
What is Engineering?
SITE MAP
Link
Pages
Contact Me
|
|
| |
Energy
Conversions: Potential Energy to Kinetic Energy
 It
started as an almost perfectly round, squishy, but not yet squished,
ball of clay.
Now it is squished - well, half squished.
Energy conversions did
it. Energy conversions do everything. Nothing can happen without
them.
In this case gravitational potential energy was converted to kinetic
energy. Kinetic energy was converted to mechanical work (force acting
through a distance - the floor pushing back against the ball).
Then finally, as is predicted by the 2nd
Law of Energy, all of the gravitational potential energy ended
up as low-grade thermal energy.
Warning: In the following discussion
there are some simple Algebra formulas. If you don't know algebra,
don't worry about it. I'll bet you will still get the gist.
 As
always, the laws of energy were demonstrated to be true, faithful,
and reliable as the US Coast Guard (in which the author once served).
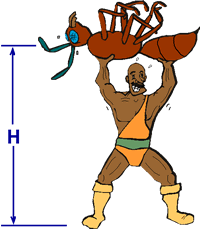
How to Smash a Clay Ball
Our friend Clayton wanted to demonstrate how to convert gravitational
potential energy to kinetic energy.
The first thing he did was pick the round ball off the floor and
lift it over his head. To do that, his hand had to exert a force
on the ball through the distance H shown in the picture. That means
work was done on the ball by his hand. The amount of work is force
times the distance the force is exerted.
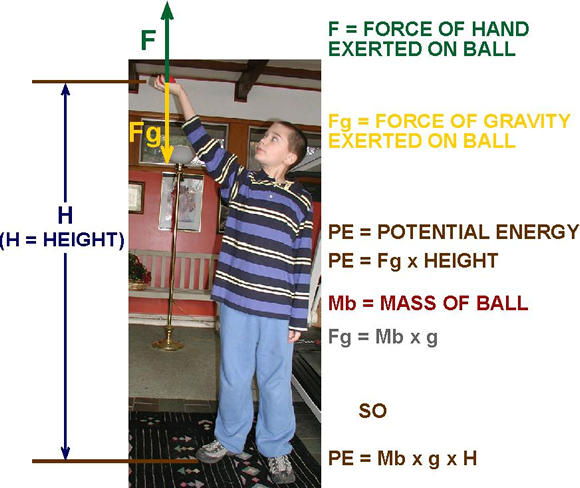
Energy is now concentrated
in the ball as gravitational potential energy. The force of gravity
is pushing the ball toward the ground, but the ball can't move because
Clayton's hand is exerting an equal force on it in the opposite
direction. The ball is not moving. No energy is being converted.
Nothing is happening.
To move the ball upward, the upward force on the ball (shown by
green arrow) had to be greater than the downward gravitational force
(yellow arrow).
If the ball is not moving it is in equilibrium.
The forces are equal and balanced.
Lifting the ball is like winding a spring. But instead of concentrating
the work into a spring, Clayton has concentrated the work into the
ball. Potential energy can be thought of as concentrated energy
waiting for its chance to flow or move to a less concentrated form
(see 2nd Law of Thermodynamics).
To lift the ball, Clayton's muscles converted concentrated food
energy into work and heat. He had to lift his body weight when he
bent over to pick up the ball; and also had to lift the weight of
his arm in addition to the weight of the ball. Since the human body
and its muscles are no more efficient than human-made machines,
only about 25% or so of the food energy was converted to work to
lift the ball. The rest of the food energy was converted into low-grade
thermal energy that heated his muscles a little, then moved into
the surrounding air. It will never be of much use to us earthlings
again.
Clayton's body used more energy to raise the ball than is now stored
in the ball - about 5 times more energy by my estimate. That is
always the way it is. We can never break even (see the 2nd
Law of Thermodynamics made easy - unless you already visited
it above).
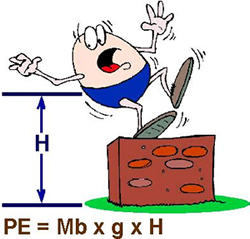 So
Clayton has managed to concentrate and store energy in the ball,
though in the process five times more "spread-out" thermal
energy was generated than ended up being concentrated in the ball.
Darn that second law.
We call the stored energy, potential energy. To be even more specific
we can call it gravitational potential energy. This tells us it
is not energy stored in a spring or in chemical bonds. It has the
potential to be converted into the energy of motion if we get the
hand force out of its way.
How much gravitational energy is stored in the ball?
In this situation the ball has the potential to fall from Clayton's
hand to the ground. If there was a deep hole under Clayton's hand
it could fall farther. But in this case it can only fall the distance
H to the ground. The
potential energy in each case depends on how far the object can
fall (not how much energy it took to raise it).
When Clayton lets go of the ball it will fall the distance H,
before its exciting, but short, trip will be stopped by the ground.
All the time the ball is falling, gravity will be pushing (or pulling?)
on it with a force equal to 9.8 m/sec^2 (meters per second squared)
times the mass of the ball. The gravitational force on the ball
is constant no matter how fast or slow the ball moves. Gravity will
exert a force I labeled Fg
on the ball for a distance H.
Work is force times distance. The work done on the ball, therefore,
is Fg times H.
That's it! That's how much potential energy is stored in the ball.
Potential Energy (PE) concentrated in the ball equals Force of Gravity
times the distance the ball will fall, or PE
= Fg x H.
If you remember Newton's laws of motion, you will remember that
Force equals mass times acceleration. In the case of gravity we
know exactly what the force is if we know the mass of the object.
We lable the acceleration caused by the force of gravity, g.
So, according to Newton,
Fg = Mb x g (Mass of
the ball times acceleration caused by gravity, g)
Now we can show a formula that always works to calculate the amount
of gravitational potential energy concentrated in an object a distance
H above
the ground:
PE
= Mb x g x H
(Potential Energy equals Mass of object times g
times Height above ground)
In this case the ball weighs 0.5 kilograms (kg). Clayton is holding
it 2 meters (m) above the ground. The acceleration caused by the
force of gravity on earth is always 9.8 meters per second squared
(m/s^2).
So,
PE
= 0.5 kg x 2 m x 9.8 m/s^2 = 9.8 Joules
That's not a lot energy, but if your nose had to absorb it, I think
it would hurt.
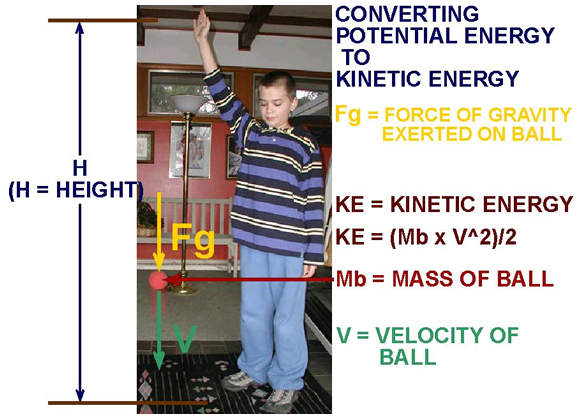
Gravity never stops pulling the ball toward the earth. The force
is constant whether the ball is falling fast or slow. That means
the rate of acceleration of the ball is constant also.
The ball speeds up (accelerates) until it hits the ground. It goes
faster and faster, until...thud! It comes to a smashing stop.
When the ball hits the ground, it has fallen the distance H.
Now its kinetic energy equals the potential energy at the start
of its fall.
After falling the distance H,
the kinetic energy equals the potential energy of Mass of the ball
times the acceleration due to gravity times the height, H.
So,
KE = (Mb x V^2)/2 = Mb x g x H
See? The Kinetic Energy at the end of the trip, is exactly equal
to the Potential Energy at the beginning of the trip.
If you know a little algebra you will be able to solve for V,
the velocity of the ball. If not, take my word for it.
Here is the answer:
V = (2gH)^1/2
...which means that after falling the distance H,
the velocity of the ball is equal to "the square root of 2
times g times H".
There you have it. Isn't that cool? If you know the mass of the
ball and the Height it is going to fall, you can calculate how fast
it will be going after falling that distance.
A Word About Air Resistance
All of the above is a bit idealized. If you are not on the moon,
or in a vacuum (gasping for air), then air resistance will eventually
slow down the ball and mess up your calculations. As every sky diver
knows, air resistance will eventually push back as hard on the ball
(or the free falling sky diver) as gravity is pulling on it. The
ball will stop speeding up (accelerating). This point is called
terminal velocity, which doesn't mean the ball has died. It means
the ball is falling at a constant speed and has stopped accelerating.
In a vacuum like outer space, the ball would keep accelerating until
something, like a planet perhaps, got in its way.
Even if air resistance slows down the ball, the potential energy
is the same (Mb x g x H). But
if air resistance is in the way, not all of the potential energy
can be converted to kinetic energy. Some of the energy has to be
used to push the air molecules out of the way. When that happens,
the energy of the air molecules is increased. The air is actually
"heated" up by the falling ball.
But for relatively short distances, we can say the air resistance
is negligible (doesn't have much effect) and our calculation is
pretty accurate.
The Final Conversion - Predictable as Always
Finally, the ball hits the ground. What happens to the kinetic energy?
As we learned in the pages on the First
Law of Energy, the energy doesn't disappear. It has to go somewhere.
All of that kinetic energy gets turned, rather quickly, through a
work process, into
thermal energy. The ball is smashed as the ball pushes on the floor
and the floor pushes back on the ball. Work is done on the ball.
If the ball hits dirt, maybe some work is done on the dirt as it
also is pushed on by the ball. The internal friction of the molecules
in the clay causes the clay to heat up.
That's right, the ball actually gets hotter. The kinetic energy
has, now, all been converted to low-grade
thermal energy. The air was heated up a little by the falling
ball, and the ball was heated up by the internal friction of the
molecules as they were pushed around during the "smashing process".
All of the potential energy was finally converted into thermal energy.
As we learned in the section on the 2nd
Law of Energy, this is what happens to mechanical energy. All
of it can be, and is eventually, converted to low-grade thermal
energy.
Once again the Laws of Thermodynamics have predicted the final end
of all energy conversions.
Summary
The amount of gravitational potential energy concentrated in an
object is determined by how far it will fall (which I called H),
how much mass it has (M),
and the acceleration due to the force of gravity, g
(it would be different on the moon than on earth).
When an object is allowed to fall, the concentrated gravitational
potential energy is converted into the kinetic energy of motion.
If there is no air resistance, or other restrictions, all of the
potential energy will be converted to kinetic energy when the object
has fallen the distance H.
The formulas to calculate potential energy and kinetic energy of
an object are simple and accurate, but it takes most of us a little
practice to get good at it.
|
|
| |
|
|
| |
If this page was helpful, please share:
|
|
|
| |
|
|
 |
|
|
|
|
|
