| |
|
Ponder
the stuff below:
|
|
|
|
|
|
|
| |
|
Let's
make up some facts about our cube creature.
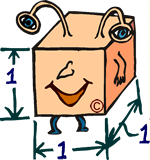
Look to the right at our first little Wild-Eyed
Blue-Legged (WEBL for short?) cube creature. Its little cube body is exactly one
cube tall and one cube wide and one cube deep.
Let's say it weighs one pound. And let's say it
can lift exactly ten pounds over its head. Pretty strong - ten times its weight
over its head. |
|
|
|
 |
|
|
| |
|
Surface Area
The surface area is important also. Each flat surface
on the outside of our cube creature is 1 flat square. So we can say the surface
area of its face is one square.
|
|
|
|
WEBL
Size 1 Cube Creature:
Height
= 1; width = 1; thickness = 1
Cross Sectional surface area of
face = 1 square
Weight = 1 pound
Weight lifted over its head =
10 pounds
It can lift 10 times its
weight over its head.
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
| |
|
|
|
|
|
|
|
|
| |
|
What
Happens When You Grow
|
|
|
|
|
TWICE AS TALL - 8 TIMES HEAVIER
|
|
|
|
| |
|
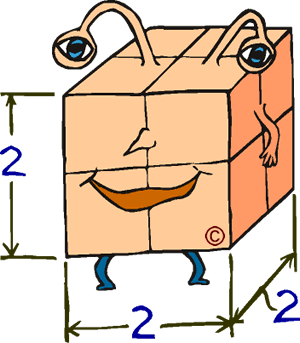
Look
at the WEBL cube creature to the right. It has grown proportionately
twice as big. It is now twice as tall, twice as wide and twice as deep.
In other words it is two cubes tall, two cubes wide,
and two cubes deep.
But look closely. It has grown twice as tall, but
its inside spaces have grown much more. Now it could fit 8 cubes of its former
self inside itself. This measure of inside space is called volume. Our cube creature
has grown twice as tall, but its volume has increased much more. Its volume is
8 times greater.
If, as we said above, each cube section weighs
1 pound, then our cube creature now weighs 8 pounds. It is now 8 times heavier!
Twice as tall but 8 times heavier!
|
|
|
|
 |
|
|
| |
|
And don't forget the surface area. Look at our creature's
face. Before, the surface area of its face was 1 flat square. Now its face has
four flat squares. It also has four times the surface area through any cross-section,
even though it only grew twice as tall.
|
|
|
|
WEBL Size 2 Cube Creature:
Height = 2; width
= 2; thickness = 2;
Cross Sectional area of face =
4 squares
Volume = 8 cubes
Weight = 8 pounds
Weight lifted over its head =
40 pounds
It can now only lift 5 times its
own weight over its head. |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
INTERMISSION TO EXPLAIN SOMETHING
|
|
|
|
| |
|
Ants
and people are shaped and built very differently. Ants have six legs, big heads
(with small brains), and huge jaws. We have two arms, two legs, small heads (with
big brains), and two arms. Ants also have their skeletons on the outside and we
have our skeletons inside.
It would be very difficult (but not impossible)
to compare ants and humans. Also, because of the way we are designed it would
not really be possible to change our sizes as much as we are talking about on
this page.
We are "over simplifying"!
Click on the above link to
read about over-simplifying.
|
|
|
|
|
"BUT WAIT!" you say, "How do
you know how much weight the Size 2 Cube Creature can lift?"
How do I know that when the Wild-Eyed Blue-Legged
Cube Creature gets 8 times heavier it can only lift 4 times as much? Now it can
lift 5 times its weight. Before, when it was half as tall, it could lift 10 times
its weight.
What changed?
Well, his weight is simply increasing faster than
his muscle strength is growing. Bio-physicists have told me in various papers
and books, that muscle strength changes approximately with the change in muscle
cross-sectional area. So that's all that has happened to our cube creature. The
cross-sectional areas have increased by a factor of four, while the weight increased
by a factor of eight.
So even though a big guy can be much stronger than
a little guy, if he is growing proportionately,
his strength can't increase as fast as his weight is increasing.
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
| |
|
|
|
|
|
|
|
|
| |
|
 |
|
|
|
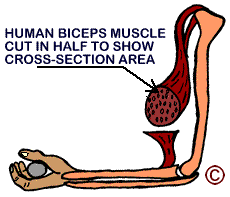
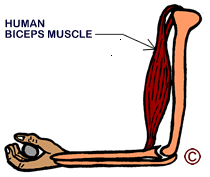
When muscles get bigger or smaller
proportionately, the force they can exert changes
mainly with the cross sectional area, not with the weight or length or width.
This is true for all animals, including ants and humans. |
|
|
| |
|
|
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
10 TIMES AS TALL - 1000 TIMES HEAVIER
|
|
|
|
| |
|
Now
look to the right at our Wild-Eyed Blue-Legged Cube Creature. It has grown ten
times taller proportionately. When we say something has grown proportionately,
we mean all the dimensions have increased by the same amount. It might be clearer
to say all the dimensions have grown in the same proportion or by the same amount.
So the WEBL to the right has grown 10 times taller, 10 times wider, and 10 times
deeper.
The same is the case with its muscles. They have
grown 10 times longer, 10 times thicker, and 10 times wider.
But look closely at the cube shaped guy. Now his
surfaces are 100 times bigger (so the cross sectional area of his muscles are
100 times bigger) and his inside volume is 1000 cubes (10 times 10 times 10).
He is 1000 times heavier!
|
|
|
|
Look! Our cube creature has 1000 cubes inside itself!
It got 10 times taller, but 1000 times heavier. Weight changes a lot faster than
height. So it is with all animals if all dimensions change in the same proportion.
|
|
|
| |
|
Those
of you that know algebra will recognize that our cube creature's (and any other
animal's) weight increases or decreases with the cube of the change in length.
So here is the bottom line. Our strange guy is ten
times taller, 100 times stronger, and 1000 times heavier
.
See what's happening. Our creation is getting stronger,
but his strength is not increasing as fast as his weight. There is nothing to
be done about it. It is a simple fact of geometry that can't be changed.

Even though his muscles are, pound for pound, every bit
as strong as they ever were, the WEBL went from being able to lift 10 times his
weight, to being just barely able to lift one times his own weight.
As you grow larger, your muscle strength grows,
but not as fast as your weight.
(And actually, for reasons partially descibed in the over simplifying
appendix below, we suspect your strength would actually increase less than is
estimated here).
| If you think you understand
the way I am doing my figuring, try doing some of your own estimates. Let me know
if I am doing this right. E-mail Me.
|
|
|
|
|
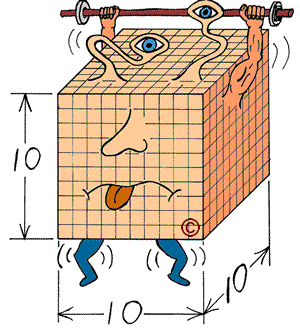
WEBL Size 10 Cube Creature:
Height = 10; Width = 10; Thickness
= 10;
Cross Sectional area = 100 squares
Volume = 1000 cubes
Weight = 1000 pounds
Weight lifted over its head =
1000 pounds
Now it can only lift 1 times its
weight.
(OK, the drawing doesn't look quite right. I should have drawn the barbell and
weights bigger. They don't look like they weigh the same as the Cube Creature,
do they?)
 |
Let's
do it for an ant.
Let's say we have an ant that is 6 millimeters long
and weighs about 3 milligrams (or 0.003 grams). This, according to one of my references,
is about the size of a leafcutter ant. Pictures of leafcutter ants carrying leaf
sections much bigger than themselves are common and they are often touted as being
super strong.
Well we found lots of claims about ant strength.
The weight lifting claims ranged from 10 to 50 times their own weight. Every one
of the sources claimed this was the equivalent of a man lifting 10 to 50
times his weight.
Let's use 50 which I suspect is on the high side for most
ants. That means our ant can lift 150 mg, or 0.15 grams.
Now let's grow our ant to 6 feet (1829 millimeters)
in length. An increase of 304.8 times the original length of 6mm. If she (most
ants are females) grows proportionally, she will
weigh about 187 pounds when she gets to 6 feet in length. Continuing to use the
relationships described above, we can calculate that this frighteningly large
ant will now be able to lift 13,935,456 milligrams. That sounds like a lot more.
But alas, it is really only 13,935 grams or just about 30.7 pounds. (see the stuff
below on over simplifying).
Now our giant ant cannot quite lift one sixth
of her body weight! No one would brag about that. And I suspect, though won't
try to prove it here, that she will not even be able to lift that. She'll be lucky
if she can lift her head.
Go Back to the Top of the Page |
 |
 |
 |
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
THIS
IS FUN! LET'S DO IT FOR PEOPLE
|
|
|
|
| |
|
If
you shrank to 6 mm tall would you be able to toss ants around like juggling pins?
The examples to the right and above would seem to
indicate that we are stronger than ants. I think we are. Even stronger, maybe,
than these estimates suggest.
I still don't think l'd want to mess with them.
Ants have those giant sharp pincher jaws and a nasty stinger on the other end,
not to mention thousands of nest mates that will eagerly come running to help
cut you up into bite sized morsels.
As we said in
Super Bugs - Part 1, the real strength of ants comes from their non-stop
determination and huge organized numbers. They're everywhere. |
|
|
|
|
Pretend
you are 6 feet tall and weigh 200 pounds. You're a pretty strong guy or girl and
can push 100 pounds worth of barbell and weights over your head. Not exactly olympic
material, but not bad. That's one half your body weight.
Seems pretty pathetic next to our leafcutter ant
that can lift and carry 50 times its weight (though I have never actually verified
this. Have you?).
(Remember we are over simplifying)
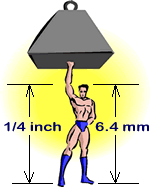
But what happens if we shrink you?
We zap you with the "Honey I Shrunk the Kids"
ray and you shrink all the way down to about 6 mm or 1/4 of an inch.
According to my estimation using the relationships described
above, you now weigh 3.2 milligrams. Based on the change in cross-sectional area
of your muscles you can now lift 488 milligrams.
That's almost 153 times your weight!
Now you are 3 times stronger than the whimpy ant!
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |







